Regular languages

Often denoted as “REG”.

Regular languages correspond to:

• Regular expressions (RE) and Regular expressions extended (REE)
• Deteremenisitc finite automata (DFA) and Non-deteremenisitc finite automata (NFA)
• Kleene algebra
  • Hence Brzozowski derivative
• Type 3 Chomsky grammar

Automata

There are a lot of algorithms to construct automata from Regular expressions:

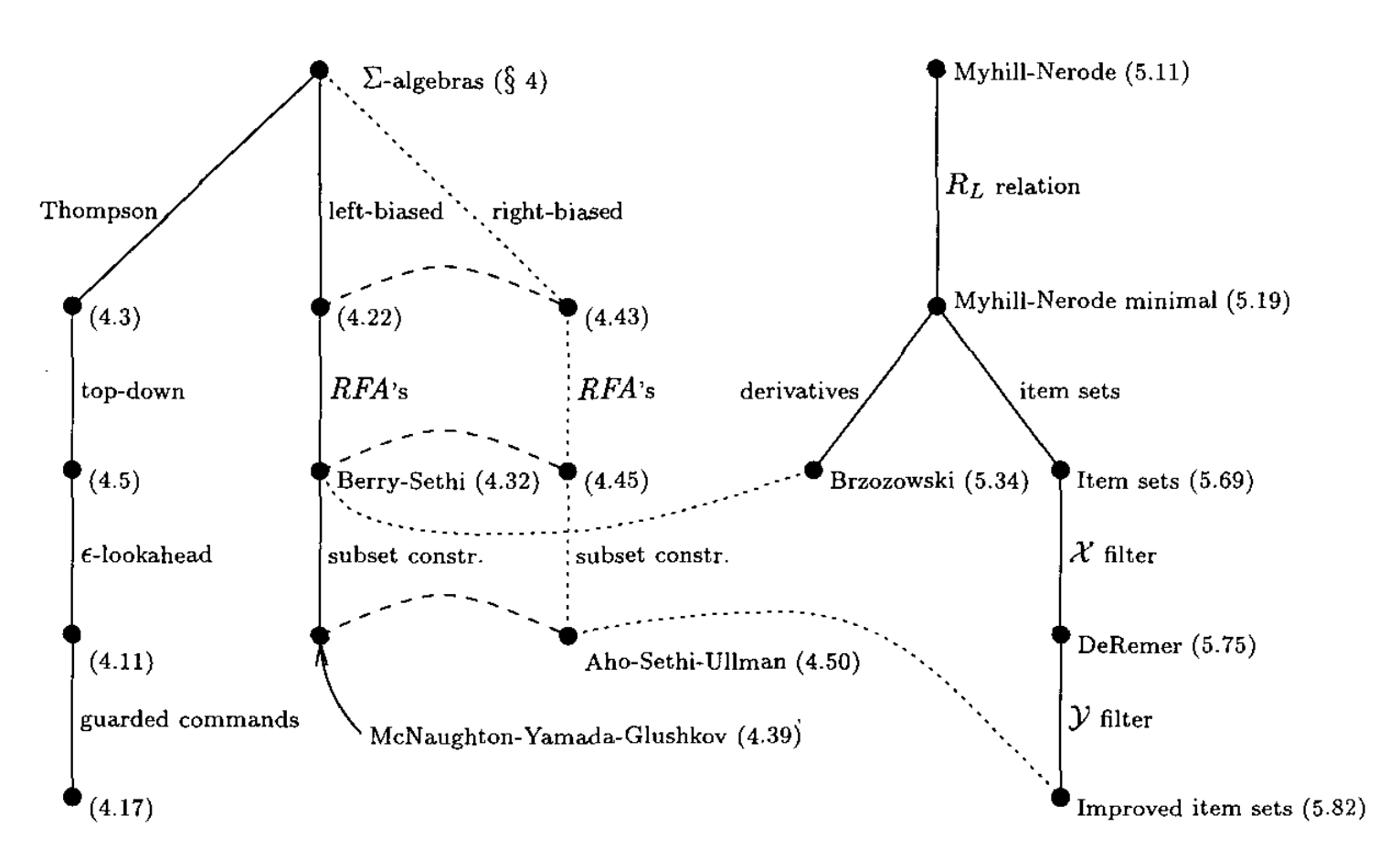
Diagram taken from A taxonomy of finite automata construction algorithms, 1995

• Myhill-Nerode construction, 1957-1959
  • MYHILL, J. “Finite automata and the representation of events,” WADD TR-57-624, pp. 112-137, Wright Patterson AFB, Ohio, 1957
  • NERODE, A. “Linear automaton transformations,” Proc. AM8 9: 541-544, 1958
  • RABIN, M.O AND D. SCOTT. “Finite automata and their decision problems,” IBM J. Res. 3(2): 115-125, 1959
• McNaughton-Yamada-Glushkov construction, 1960-1961
  • McNAUGHTON, R. AND H. YAMADA. “Regular expressions and state graphs for automata,” IEEE Trans. on Electronic Computers 9(1): 39-47, 1960.
  • GLUSHKOV, V.M. “The abstract theory of automata,” Russian Mathematical Surveys 16: 1-53, 1961
  • An optimal parallel algorithm to convert a regular expression into its Glushkov automaton, 1999
  • Characterization of Glushkov automata, 2000
• Brzozowski construction, 1964
  • BRZOZOWSKI, J.A. “Derivatives of regular expressions,” J. ACM 11(4): 481-494, 1964
  • Regular-expression derivatives re-examined, 2009
  • Manipulation of Extended Regular Expressions with Derivatives, 2015
• Thompson’s construction, 1968
  • THOMPSON, K. “Regular expression search algorithms,” C. ACM 11(6): 419-422, 1968
• DeRemer’s construction, 1974
  • DEREMER, F.L. “Lexical analysis,” in Compiler Construction: an Advanced Course, (F.L. Bauer and J. Eickel, eds.), pp. 109-120, Lecture Notes in Computer Science 21, Springer-Verlag, Berlin, 1974
• Berry-Sethi construction, 1986
  • BERRY, G. AND R. SETHI. “From regular expressions to deterministic automata,” Theoretical Computer Science, 48: 117-126, 1986.
• Aho-Sethi-Ullman DFA construction, 1986
  • AHO, A.V., R. SETHI, AND J.D. ULLMAN. Compilers: Principles, Techniques, and Tools, Addison-Wesley Publishing Co., Reading, M.A., 1988
• Antimirov construction, 1996
  • Partial derivatives of regular expressions and finite automaton constructions, 1996
  • Antimirov and Mosses’s Rewrite System Revisited, 2008
  • Symbolic Solving of Extended Regular Expression Inequalities, 2014
• Follow automata, 2003
  • A Unified Construction of the Glushkov, Follow, and Antimirov Automata, 2006
• Tree automata, 2011
• Counting-set automata, 2020
• Bit vector automata, 2023

Other:

• A simple way to construct NFA with fewer states and transitions, 2004
• Bitwise Data Parallelism in Regular Expression Matching, 2014
• PaREM: A Novel Approach for Parallel Regular Expression Matching, 2014

Regular expressions

RE

Regular expression can be defined recursively:

$$r ::= \alpha | \epsilon | r_1 r_2 | r_1 + r_2 | r_1^* | (r_1)$$

Let assume that $L(r)$ is languages defined by regulat expression $r$ then:

• $L(\alpha) = \{ \alpha \}$, where $\alpha \in \Sigma$ and $\Sigma$ is alphabet of the language. Examples: L(a) = { "a" }, L(b) = { "b" }, etc.
• $L(\epsilon) = \{ \varepsilon \}$, where $\varepsilon$ is empty string. Example: L(ϵ) = {""}
• $L(r_1 r_2) = L(r_1) \times L(r_2)$, where $L(r_1) \times L(r_2)$ is cartesian product of sets. Examples: L(ab) = { "a" }×{ "b" } = { "ab" }, L(ba) = { "ba" }, etc.
• $L(r_1 + r_2) = L(r_1) \cup L(r_2)$, where $L(r_1) \cup L(r_2)$ is union of languages (union of sets). Examples: L(a + b) = { "a", "b" }, L(b + a) = { "b", "a" }, etc.
• $L(r_1^*) = L(r_1)^*$, where $L(r_1)^*$ is Kleene closure (star). Example, L(a*) = {"", "a", "aa", "aaa"...}
• $L((r_1)) = L(r_1)$. Parentheses used for grouping
• For convienience we can also define, $L(\empty) = \{\}$

Variation of notation:

	RE	sets	Chomsky	Kleene algebra
concatenation	$r_1 r_2$	$r_1 \times r_2$	$r_1 r_2$	$r_1 \cdot r_2$
alternation (1)	$r_1 + r_2$	$r_1 \cup r_2$	r_1 | r_2	$r_1 + r_2$
empty string (2)	$\epsilon$ or $\varepsilon$	$\{ \varepsilon \}$	$\epsilon$ or $\varepsilon$	$1$
empty language	$\empty$	$\empty$ or $\{\}$		$0$
Kleene closure	$r^*$	$r^*$		$r^*$

• (1) other name for alternation is unordered choice
• (2) in older books they may use $\lambda$ for empty string

REE

Extended regular expression can be defined recursively:

$$r ::= \alpha | \epsilon | r_1 r_2 | r_1 + r_2 | r_1^* | (r_1) | r_1 \& r_2 | r_1'$$

REE is the same as RE, but with two additonal operations intersection ($\&$) and negation ($r_1'$).

• $L(r_1 \& r_2) = L(r_1) \cap L(r_2)$, where $L(r_1) \cap L(r_2)$ is intersection of sets.
• $L(r_1') = L(r_1)'$, where $L(r_1)'$ is absolute complement of a set.

Variation of notation:

	REE	sets	Logic
concatenation	$r_1 r_2$	$r_1 \times r_2$
alternation	$r_1 + r_2$	$r_1 \cup r_2$	$r_1 \lor r_2$
empty string	$\epsilon$ or $\varepsilon$	$\{ \varepsilon \}$
empty language	$\empty$	$\empty$ or $\{\}$	$\bot$
Kleene closure	$r^*$	$r^*$
intersection	$r_1 \& r_2$	$r_1 \cap r_2$	$r_1 \land r_2$
negation	$r'$	$r'$ or $r^c$ or $U \setminus r$	$\lnot r$
universe	$\Sigma^*$	$U$	$\top$

Modern syntactic sugar

Modern regular expressions “engines” support several more extensions for convenience (aka syntactic sugar):

• “Kleene plus” in plain text notation r+ = $r r^*$
• “Kleene question” in plain text notation r? = $r + \epsilon$
• Quantifiers
  • r{n} = $\underbrace{r \ldots r}_{n\text{-times}}$
  • r{n,m} = $\underbrace{r \ldots r}_{n\text{-times}}\underbrace{(r+\epsilon) \ldots (r+\epsilon)}_{(m-n)\text{-times}}$
  • r{n,} = $\underbrace{r \ldots r}_{n\text{-times}}r^*$
  • r{,n} = $\underbrace{(r+\epsilon) \ldots (r+\epsilon)}_{n\text{-times}}$
• Any character: . = $\Sigma$
• Interval: [a-z] = $a + \ldots + z$
• Set: [abc] which is the same as a|b|c = $a + b + c$
• Negation of set: [^abc] = $\Sigma \setminus (a + b + c)$
• Char classes, for example:
  • \d is the same as [0-9] = $0 + \ldots + 9$
  • \w, \s, \S etc.

RELA

See RE with lookahead

RE with backreferences

Some modern regular expressions “engines” may contain extensions which do not correspond to regular languages - see RE with backreferences.

Related

• Brzozowski derivative
• Antimirov partial derivative

References

• CS4114 Formal Languages Spring 2021, Chapter 4 Regular Languages
• Foundations of Computation (Critchlow and Eck), 3.2: Regular Expressions

Kleene algebra

A Kleene algebra is an algebraic structure

$$K = (\Sigma, +, \cdot, {}^*, 0, 1)$$

satisfying the following equations and equational implications:

$$\begin{align} a + (b + c) &= (a + b) + c \\ a + b &= b + a \\ a + 0 &= a \\ a + a &= a \\ a(bc) &= (ab)c \\ 1a &= a \\ a1 &= a \\ a(b + c) &= ab + ac \\ (a + b)c &= ac + bc \\ 0a &= 0 \\ a0 &= 0 \\ 1 + aa^* &\leq a^* \\ 1 + a^*a &\leq a^* \\ b + ax \leq x &\implies a^*b \leq x \\ b + xa \leq x &\implies ba^* \leq x \\ \end{align}$$

where $\leq$ refers to the natural partial order on $K$:

$$a \leq b \iff a + b = b$$

• Axioms 1-4 say that $(\Sigma, +, 0)$ is an idempotent commutative monoid.
• Axioms 5-7 say that $(\Sigma, \cdot, 1)$ is a monoid.
• Axioms 1-11 say that $(\Sigma, +, \cdot, 0, 1)$ is an idempotent semiring.

References

• A Completeness Theorem for Kleene Algebras and the Algebra of Regular Events
• KLEENE ALGEBRAS: THE ALGEBRA OF REGULAR EXPRESSIONS

Closure properties

TODO

Decidability

TODO

Pumping lemma

TODO